Patcher
Description
This functor generates new patches of a certain class or category using a seeding mechanism.
Inputs
| Name | Type | Description |
|---|---|---|
| Landscape | Categorical Map Type | Map of classes or categories. |
| Probabilities | Map Type | Map of spatial probabilities. |
| Changes | Change Matrix Type | Matrix of number of changes. |
| Transition Parameters | Transition Function Parameter Matrix Type | Matrix of transition function parameters consisting of Mean Patch size, Patch size variance, and isometry. By varying these parameters, various spatial patterns can be reproduced (see examples on Patterns of Change). Increase the patch size for a less-fragmented landscape. Increase the patch size variance for a more diverse landscape, and set isometry greater than one for more isometric patches. Tipically, the isometry defines the aggregation level of a patch. Assuming that v is the current isometry value, 0<v<1 forces disaggregation, v>1 forces aggregation and v=1 is ignored. The mean patch size and the variance define the size of the new patches. |
Optional Inputs
| Name | Type | Description | Default Value |
|---|---|---|---|
| Neighbor Window Lines | Positive Integer Value Type | Number of lines and columns of the neighbor search window. Patches can be created in a diffuse way by increasing the neighbor search window to values greater than 3 for lines and columns; a 3×3 window corresponds to the Moore neighborhood. | 3 |
| Neighbor Window Columns | Positive Integer Value Type | 3 | |
| Prune Factor | Real Value Type | A multiple of the quantity of cells to be changed. This is used in order to specify the size of the vector where cells are ranked for subsequent draw. Prune factor multiplies the expected number of cells to be changed to set the quantity of possible cells, based on their spatial probability, that take part in the selection mechanism of new patch nuclei. Typically, increasing this value also increases the stochasticity of selection of patch pivot cells. | 10 |
Outputs
| Name | Type | Description |
|---|---|---|
| Changed Landscape | Categorical Map Type | Map of classes or categories. |
| Corroded Probabilities | Map Type | Map of depleted spatial probabilities. Where a change occurred, the probability value is set to zero. |
| Remaining Changes | Change Matrix Type | Matrix of number of remaining number of changes for each type of transition in case the functor does not succeed in making all the specified changes. |
Group
Notes
Dinamica EGO uses as a local CA rule in its transition engine composed of two complementary transition functions, the Expander and the Patcher. Dinamica EGO splits the cell selection mechanism into these processes. The first process is dedicated only to the expansion or contraction of previous patches of a certain class, and it is called Expander. The second process is designed to generate or form new patches through a seeding mechanism, and it is called Patcher. The Patch Isometry is a number varying from 0 to 2. The patches assume a more isometric form as this number increases. The size of new patches and expansion fringes are set according to a lognormal probability distribution. Therefore, it is necessary to specify the parameters of this distribution represented by the mean and variance of the patch sizes to be formed. The combination of Dinamica EGO's transition function presents numerous possibilities with respect to the generation and evolvement of spatial patterns of change.
The Patcher function searches for cells around a chosen location for a combined transition. This is done firstly by electing the core cell of the new patch and then selecting a specific number of cells around the core cell, according to their Pij transition probabilities, as depicted below:
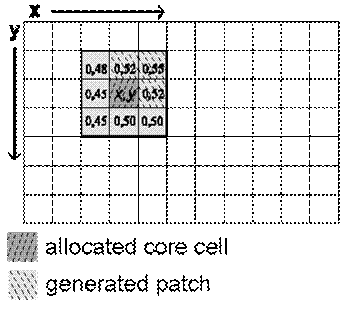
See Patterns of Change for different examples of patches generated using Patcher and Expander.
Internal Name
Patcher